2023年9月28日 / 最終更新日時 : 2023年9月28日 --- コラム

コンピュータビジョン: PnP問題って何？

コンピュータービジョンでは、PnP問題という単語が度々登場します。PnP問題とはなにか、を数学を用いずに、主に論文の引用を用いて紹介します。すべての論文にリンクをつけていますので、詳細を知りたい方はそちらをご覧ください。

はじめに

LiDAR（Light Detection and Ranging）センサーなどをもちいて、現実世界の3D座標を得たとします。その後、その機器（ドローンなど）に固定搭載されているカメラの位置と方向を知ることができれば、グローバル座標系における自らの位置を知ることができます。

PnPとは、カメラの位置と姿勢（向き）を計算することであり、「問題」というわれる所以は、この計算を効率的かつ正確に行う方法が複数存在するためです。

いかに計算負荷を低くし、正確な近似値を求められるか？、が盛んに研究されています。

Imagine you took an image of your house and showed it to your friend, and asked a simple question “Can you tell me where this photograph is taken from?”. Will your friend be able to guess the spot? If yes, then how? How our brain works to figure out the location of the camera, just by looking at the image?

Well, this is a well-known problem in Photogrammetry, known as Perspective-n-Point (PnP) problem.

訳：
自分の家の画像を撮って友達に見せ、「この写真がどこから撮られたのか教えてもらえますか?」という簡単な質問をしたと想像してください。”。あなたの友達はその場所を推測できるでしょうか？「はい」の場合、どのようにして? 画像を見るだけで、私たちの脳はどのようにしてカメラの位置を把握するのでしょうか?

これは、 Perspective-n-Point (PnP)問題として知られる、写真測量におけるよく知られた問題です。
https://medium.com/@rashik.shrestha/perspective-n-point-pnp-f2c7dd4ef1edより引用

Locating 3D objects from a single RGB image via Perspective-n-Point (PnP) is a long-standing problem in computer vision.
EPro-PnP: Generalized End-to-End Probabilistic Perspective-n-Points for Monocular Object Pose Estimationより引用

訳：
Perspective-n-Point (PnP) を介して単一の RGB 画像から 3D オブジェクトを見つけることは、コンピューター ビジョンにおける長年の問題です。


Introduction
“Camera pose estimation is a fundamental problem that is used in a wide variety of applications such as autonomous driving and augmented reality.
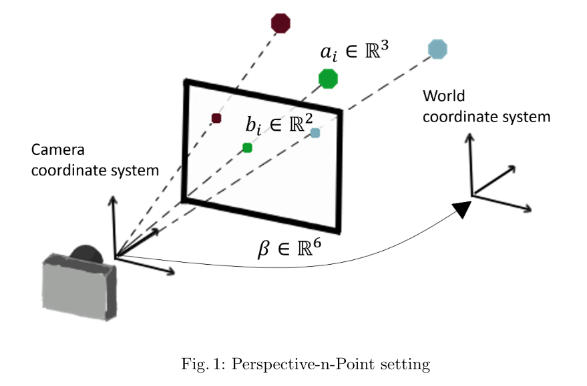
The goal of perspective-n-point (PnP) is to estimate the pose parameters of a calibrated camera given the 3D coordinates of a set of objects in the world and their corresponding 2D coordinates in an image that was taken (see Fig. 1).
Currently, PnP can be efficiently solved under both accurate and low noise conditions [15,17]. In practice, there may be wrong data associations within the 2D and 3D pairs due to missing objects or incorrect object recognition. Therefore, the main challenge is to develop robust PnP algorithms that are resilient to these imperfections. Identifying outliers is a computationally intensive task which is impractical using classical model based solutions. The goal of this paper is therefore to derive a hybrid approach based on deep learning and classical methods for efficient and robust PnP.”

訳：
“カメラの位置姿勢の推定は、自動運転や拡張現実など、さまざまなアプリケーションで使用される基本的な問題です。
perspective-n-point（PnP）の目標（ゴール）は、キャリブレーションされたカメラの位置姿勢パラメータを現実世界のオブジェクト3D座標と、それらの対応する2D座標（撮影された画像内で）で推定することす（図1を参照）。
現在、PnPは正確で低ノイズの条件下で効率的に解決できます[15,17]。実際には、2Dと3Dのペア内で誤ったデータの関連付けがあるかもしれません。これは、オブジェクトが欠落したり、不正確なオブジェクト認識があるためです。したがって、主要な課題は、これらの不完全さに耐える堅牢なPnPアルゴリズムを開発することです。外れ値を特定することは、古典的なモデルベースの解決策を使用して実用的ではない計算集約的なタスクです。したがって、この論文の目標は、効率的で堅牢なPnPのための深層学習と古典的な方法に基づくハイブリッドアプローチを導くことです。”
PnP-Net: A hybrid Perspective-n-Point Networkより引用

“The aim of the Perspective-n-Point problem—PnP in short—is to determine the position and orientation of a camera given its intrinsic parameters and a set of n correspondences between 3D points and their 2D projections. It has many applications in Computer Vision, Robotics, Augmented Reality and has received much attention in both the Photogrammetry (McGlove et al. 2004) and Computer Vision (Hartley and Zisserman 2000) communities. In particular, applications such as feature point-based camera tracking (Skrypnyk and Lowe 2004; Lepetit and Fua 2006) require dealing with hundreds of noisy feature points in real-time, which requires computationally efficient methods.”

EPnP: An Accurate O(n) Solution to the PnP Problemより引用

訳：
「Perspective-n-Point問題」、略して「PnP」とも呼ばれるこの問題の目的は、カメラの位置と姿勢を決定することです。そのためには、カメラの内部パラメータと、3Dポイントとそれらの2D投影との間のn個の対応関係が必要です。これは、コンピュータビジョン、ロボティクス、拡張現実などの多くのアプリケーションで使用されており、写測法: Photogrammetry（McGlove et al. 2004）およびコンピュータビジョン（Hartley and Zisserman 2000）のコミュニティで多くの注目を集めています。特に、特徴点ベースのカメラトラッキング（Skrypnyk and Lowe 2004; Lepetit and Fua 2006）などのアプリケーションでは、リアルタイムで数百ものノイズのある特徴点を扱う必要があり、計算効率の良い手法が求められます。」

参考動画


Perspective n-point problem(YouTube)

参考文献

さまざまな解法と実装

Related Work
PnP is a fundamental problem in computer vision and has a long history of parameter estimation methods. We refer the reader to [16] for a comprehensive review. Below, we briefly review the leading algorithms along with their pros and cons.

訳：
PnPはコンピュータビジョンにおける基本的な問題であり、パラメーターの推定方法には長い歴史があります。包括的なレビューは、[16]を参照。以下では、主要なアルゴリズムを簡単に説明し、それらの利点と欠点について触れます。
PnP-Net: A hybrid Perspective-n-Point Networkより引用

DLT法（Direct Linear Transform法）、P3P法、EPnP法（Efficient Perspective-n-Point法）、その他、深層学習系。

各手法について典型的なコード（もしくは疑似コード）を紹介します。

rvec, tvecについて

rvecとtvecは、カメラの姿勢（位置と向き）を表すためのパラメーターです。

  • rvec（Rotation Vector）: 回転ベクトル。このベクトルの方向が回転軸であり、その大きさが回転角度（ラジアン）を表します。3×1のベクトルで表されます。
  • tvec（Translation Vector）: 平行移動ベクトル。カメラの世界座標系における位置（x, y, z）を表します。これも3×1のベクトルで表されます。

これらのパラメーターは、3Dの点群とそれに対応する2Dの点群、そしてカメラの内部パラメーターを用いて、cv2.solvePnPなどの関数で計算されます。

参考

1. DLT法（Direct Linear Transform法）

DLT法は、線形代数の手法を用いてカメラの姿勢を推定します。

import numpy as np
import cv2

# 3D点群
object_points = np.array([[0, 0, 0], [1, 0, 0], [0, 1, 0], [0, 0, 1]], dtype=np.float32)

# 2D点群
image_points = np.array([[100, 100], [200, 100], [150, 200], [100, 150]], dtype=np.float32)

# カメラ行列（仮定）
camera_matrix = np.array([[500, 0, 320], [0, 500, 240], [0, 0, 1]], dtype=np.float32)

# DLT法
_, rvec, tvec = cv2.solvePnP(object_points, image_points, camera_matrix, None, flags=cv2.SOLVEPNP_DLS)

print("Rotation Vector:", rvec)
print("Translation Vector:", tvec)

2. P3P法

P3P法は、3つの対応点からカメラの姿勢を推定します。

# P3P法
_, rvec, tvec = cv2.solvePnP(object_points[:3], image_points[:3], camera_matrix, None, flags=cv2.SOLVEPNP_P3P)

print("Rotation Vector:", rvec)
print("Translation Vector:", tvec)

3. EPnP法（Efficient Perspective-n-Point法）

効率的とされている計算法。EPnP: An Accurate O(n) Solution to the PnP Problem
通常のPnPソルバーはO(n^4)の計算時間が必要ですが、EPnPはO(n)の時間複雑度で解決するアルゴリズムです。

# EPnP法
_, rvec, tvec = cv2.solvePnP(object_points, image_points, camera_matrix, None, flags=cv2.SOLVEPNP_EPNP)

print("Rotation Vector:", rvec)
print("Translation Vector:", tvec)

4. 深層学習系

PnP-Net

PnP-Net: A hybrid Perspective-n-Point Networkの疑似コード。

import torch
import torch.nn as nn

class PnPNet(nn.Module):
    def __init__(self):
        super(PnPNet, self).__init__()
        self.fc1 = nn.Linear(6, 128)  # 3D-2D対応点を入力とする
        self.fc2 = nn.Linear(128, 64)
        self.fc3 = nn.Linear(64, 6)  # 回転と平行移動（姿勢）を出力する

    def forward(self, x):
        x = torch.relu(self.fc1(x))
        x = torch.relu(self.fc2(x))
        x = self.fc3(x)
        return x

# ダミーデータ
input_data = torch.rand(10, 6)  # 10個の3D-2D対応点

# モデルのインスタンス化と順伝播
model = PnPNet()
output = model(input_data)

# 出力はカメラの姿勢（回転と平行移動）
print(output)

Deep_blind_PnP

このリポジトリには、Learning 2D–3D Correspondences To Solve The Blind Perspective-n-Point Problemという論文に基づいた実装コードが公開されています。
config.pyを参照して、コマンドライン引数を指定できます。

論文のアブスト
Conventional absolute camera pose via a Perspective-n-Point (PnP) solver often assumes that the correspondences between 2D image pixels and 3D points are given. When the correspondences between 2D and 3D points are not known a priori, the task becomes the much more challenging blind PnP problem. This paper proposes a deep CNN model which simultaneously solves for both the 6-DoF absolute camera pose and 2D–3D correspondences. Our model comprises three neural modules connected in sequence. First, a two-stream PointNet-inspired network is applied directly to both the 2D image keypoints and the 3D scene points in order to extract discriminative point-wise features harnessing both local and contextual information. Second, a global feature matching module is employed to estimate a matchability matrix among all 2D–3D pairs. Third, the obtained matchability matrix is fed into a classification module to disambiguate inlier matches. The entire network is trained end-to-end, followed by a robust model fitting (P3P-RANSAC) at test time only to recover the 6-DoF camera pose. Extensive tests on both real and simulated data have shown that our method substantially outperforms existing approaches, and is capable of processing thousands of points a second with the state-of-the-art accuracy.

訳：
従来の絶対カメラ姿勢（カメラの全体的な位置と姿勢）は、Perspective-n-Point（PnP）ソルバーを通じて、2D画像ピクセルと3D点との対応関係が与えられているとしばしば仮定されます。2Dと3D点との対応関係が事前に知られていない場合、このタスクははるかに挑戦的なブラインドPnP問題となります。本論文では、6-DoFの絶対カメラ姿勢と2D-3D対応関係の両方を同時に解く深層CNNモデルを提案します。我々のモデルは、3つのニューラルモジュールが順番に接続されています。まず、PointNetに触発された二つのストリームのネットワークが、2D画像のキーポイントと3Dシーンの点に直接適用され、局所的および文脈的な情報を活用して識別的な点ごとの特徴を抽出します。次に、全体的な特徴マッチングモジュールが、すべての2D-3Dペア間のマッチング可能性行列を推定するために使用されます。最後に、得られたマッチング可能性行列は、インライアマッチを明確化するための分類モジュールに供給されます。ネットワーク全体はエンドツーエンドで訓練され、テスト時にのみ堅牢なモデルフィッティング（P3P-RANSAC）が行われて、6-DoFカメラ姿勢を回復します。実際のデータとシミュレーションデータの両方での広範なテストにより、我々の方法は既存のアプローチを大幅に上回り、最先端の精度で秒間数千点を処理できることが示されています。

まとめ

PnP問題とはなにか、を主に論文の引用を用いて紹介しました。
すべての論文にリンクを貼りましたので、詳細を知りたい方はそちらをご覧ください。

以上です。ありがとうございました。

カテゴリー
コラム
タグ
コラム

前の記事

カメラキャリブレーションのABC: 知っておきたい基本
2023年9月21日
コラム

次の記事

NumPyからCuPyへ：高速化の一例
2023年9月28日