コサイン類似度データの中の外れ値をもつファイルを見つける方法

はじめに
皆さん、画像分類、やってますか?
世の中は大規模言語モデルや動画生成AIが話題の中心になっていますが、画像分類、特にオープンセット分類^0の需要はますます高まっています。
引用:Open Vision (NSF IIS-1320956)
そのようなオープンセット分類に、例えば顔認証があります。日本人の顔認識に使う学習モデルのひとつに、拙作のJAPANESE FACE v1があります。日本人専用にチューニングしてありますので、日本人の顔に対する感度が優れています。この学習モデルはいわゆるコミュニティーライセンスですので^1、顔認識に使ってください。
さて、顔学習モデルを作成するにあたり、集められたデータセットのクレンジングには相当気を使います。
下の図はヒョウの分類です。ヒョウを分類する学習モデルを作成しようとした場合、そのデータセットのクレンジングには、特に気を使わなければなりません。
例えばアムールヒョウのフォルダにアラビアヒョウの画像ファイルが入っていてはいけないのです。

この場合(アムールヒョウのフォルダにアラビアヒョウの画像ファイルが入っている場合)で言うと、アラビアヒョウの画像ファイルが「外れ値」をもつファイルということになります。
顔認証のための学習データであれば、例えば1つのディレクトリに複数の同一人物の異なる顔画像ファイルがあったとき、もしかしたら別人の顔画像がふくまれているかも知れません。(同姓同名の違う人物の顔画像ファイルが紛れている場合)
あるいは、別人とは言わないまでも、顔データセットとしてふさわしくない画像かも知れません。(顔加工ソフトによって修正された顔画像ファイルなど)
外れ値を持つ画像ファイルを探し出して除去することは、学習データを堅牢な物にするためにとても重要です。
1つのディレクトリならば目視すればよいですが、何百何千とディレクトリ(=クラス)が存在るのであれば、自動化するべきです。
この記事では、コサイン類似度を使って複数の顔画像から生成したベクトルの中で「外れ値」を見つけるためのさまざまな方法について吟味します。
各手法の概要、メリット・デメリット、そしてグラフ化して視覚化する場合の手法を共有します。
実際のコードでは、顔認証フレームワークであるFACE01^2を用います。こちらもいわゆるコミュニティーライセンスとなっています。
本来同一のクラスにしなくてはいけないのに異なるクラスになっている場合のチェックは、「【faiss】なにこれすごい。顔データセットの間違い探し 成功編③」を参照してください。
https://zenn.dev/ykesamaru/articles/4e40e0285b0b66
使用する顔画像データセット

[!NOTE]
なおこの記事で取り扱う画像ファイルは記事を作成するための例であって、このサンプルを使って顔学習モデルを作製しているわけではないことをおことわりします。
補足:コサイン類似度と計算
釈迦に説法になりますが、おさらいとしてコサイン類似度の定義と類似度の計算方法を補足として記述します。この部分が不要な方は次の章へスキップしてください。
コサイン類似度は2つのベクトル間の角度のコサイン値を計算することで類似度を評価する場合に用いられます。
値は-1から1までの範囲を取りますが、顔認識などの特徴ベクトルにおいては、通常0から1の範囲で1に近いほど似ていると評価されます。
2つのベクトル $a$ と $b$ のコサイン類似度は次の式で定義されます。
$$ \cos(\theta) = \frac{\mathbf{a} \cdot \mathbf{b}}{||\mathbf{a}|| \times ||\mathbf{b}||} $$
- $a \cdot b$ は、ベクトル $a$ と $b$ の内積です。
- $||a||$と $||b||$は、それぞれのベクトルのノルム(長さ)です。
その1: ベクトルの内積の計算
2つのベクトル $a$ と $b$ の内積は、2つのベクトルの対応する要素を掛け合わせたものを全て足し合わせて求めます。
$$
\mathbf{a} \cdot \mathbf{b} = a_1 \times b_1 + a_2 \times b_2 + \dots + a_n \times b_n
$$
2つのベクトルが同じ方向を向いているときに大きな値が得られ、関係ない方向に向いているときには小さな値や負の値になります。
その2: 各ベクトルのノルムを計算
次にベクトル $a$ と $b$ のノルム(大きさ)を計算します。各ノルムは、各要素を2乗して合計した数の平方根をとることで得られます。
$$||\mathbf{a}|| = \sqrt{a_1^2 + a_2^2 + \dots + a_n^2}$$
$$
||\mathbf{b}|| = \sqrt{b_1^2 + b_2^2 + \dots + b_n^2}
$$
その3: コサイン類似度を求める
最後に、内積の値を2つのノルムの積で割ることで、コサイン類似度を求めます。
$$
\cos(\theta) = \frac{\mathbf{a} \cdot \mathbf{b}}{||\mathbf{a}|| \times ||\mathbf{b}||}
$$
この計算によって得られる値が、2つのベクトル間のコサイン類似度です。
コサイン類似度データから外れ値を見つける方法
平均と標準偏差による閾値設定
概要
コサイン類似度の平均と標準偏差を用いて、平均から一定の標準偏差を超える点を外れ値として判定します。
閾値の設定
この手法ではコサイン類似度の平均と標準偏差を使って、異常なデータ点を「平均から一定の標準偏差の距離を超える点」とします。
$$
\text{閾値} = \text{平均} \pm k \times \text{標準偏差}
$$
( k )は調整パラメータで、一般的には1.5や2、あるいは3がよく使用されるようです。例えば( k = 2 )と設定すれば、コサイン類似度が平均から2標準偏差以上離れたデータ点を外れ値とみなします。
メリット
- 単純で実装が容易。
- データの分布を直感的に利用できる。
デメリット
- データの分布に依存しすぎるため、正規分布に近い形状のデータセットで有効ですが、極端に歪んだ分布(例えば偏りが大きい場合)では外れ値が検出できない場合があるようです。
k-Nearest Neighbors (k-NN) の距離による外れ値検出
概要
k近傍法を用いて、各データ点の近隣とのコサイン距離を評価し、その距離が一定の閾値を超えるものを外れ値とします。
コサイン距離は、コサイン類似度を距離の概念に変換したものです。一般的には以下のように定義されます。
$$
\text{コサイン距離} = 1 – \cos(\theta)
$$
コサイン距離は0から2の範囲を取り、値が小さいほどベクトル間の類似性が高い(距離が近い)ことを示します。
k-NN法やクラスタリングなどのアルゴリズムでは、データ間の「距離」を測る必要があります。コサイン類似度は類似性の指標であるため、そのままでは距離計量として適用しにくいです。そこで、類似性を距離に変換するためにコサイン距離を使用します。
ユークリッド距離では適切な距離を測れない場合でも、コサイン距離はベクトルの方向性を重視するため、より適切な類似度評価が可能です。
この手法では、各データ点の近傍とのコサイン距離を計算し、距離が大きい(すなわち、類似性が低い)データ点を外れ値として検出します。
メリット
- 局所的な距離関係を考慮できるため、データのパターンを捉えやすい。
- 高い精度が期待できる。
デメリット
- 計算コストが高く、大規模データには不向き。
- kの選び方によって結果が左右されやすい。
局所外れ値因子 (Local Outlier Factor, LOF)
概要
LOFとは各データ点の周囲の密度を基準にして、他の点と比べてどれだけ「外れ」ているかを評価する手法です。
外れ値をデータ全体のグローバルな視点ではなく、各点の「局所的な密度」に基づいて評価するため、、データ全体の平均や標準偏差を使用する方法よりも、密度が異なるクラスターを含むデータセットに対して有用と言えそうです。
通常のLOFではユークリッド距離を使用して近傍点を決定しますが、ここではコサイン距離を用います。先述しましたがコサイン距離は、コサイン類似度を基に次のように計算されます。
$$
\text{コサイン距離} = 1 – \cos(\theta)
$$
このコサイン距離は2つのベクトルの角度の違いを反映した距離であり、2つのベクトルが近い(類似性が高い)場合は0に近く、異なる方向にあるほど1に近づきます。
LOFの計算手順
- 各点の( k )近傍点をコサイン距離で決定
- 各データ点に対して指定した( k )個の近傍点までの距離(k近傍距離)を算出。このk近傍には、512次元ベクトルに対する各点のコサイン距離が最も小さい順にk個のデータ点を選びます。
- 具体的にはユーザー設定パラメータ( k )は、通常は小さな値(例:5〜20)に設定します。
- 到達可能距離(Reachability Distance)の計算
- データ点Aとその近傍点Bに対して「到達可能距離」を算出。
- 具体的には、到達可能距離は「BからAへの距離」と「Bのk近傍距離」のうち大きい方を採用します。
\text{到達可能距離} = \max(\text{k近傍点のコサイン距離}, \text{他の点とのコサイン距離})
$$
- 局所密度の計算
- 各データ点に対してその周囲の点の到達可能距離の逆数を取ることで局所密度を算出。
- 局所密度が高い点は「密集したエリアにある点」、低い点は「孤立したエリアにある点」を意味します。
\text{局所密度} = \frac{k}{\sum_{i=1}^{k} \text{到達可能距離}(i)}
$$
- LOFスコアの計算
- 各データ点の局所密度を周囲の点の局所密度と比較して、LOFスコアを算出します。
- LOFスコアが1に近いほど、その点は周囲と似た密度であるため通常のデータと見なされます。
- スコアが1より大きい場合、その点は周囲に比べて密度が低く、「外れ値」として扱われやすくなります。スコアが2や3に近づくほど、より強い外れ値と判断されます。
\text{LOFスコア} = \frac{\text{他の近傍点の局所密度の平均}}{\text{自身の局所密度}}
$$
メリット
- 局所的な密度を基準とするため、異なる密度を持つクラスタが存在しても外れ値をうまく検出できる。
デメリット
- パラメータ調整が難しく、適切な近隣数を選ぶ必要がある。
- 大規模データセットでの計算負荷が大きい。
- ( k )の設定が結果に影響を与えるため、適切なパラメータ調整が重要(( k )を小さくしすぎるとノイズの影響を受けやすくなり、大きくしすぎると局所性が失われる。)
FAISSを使った外れ値検出
FAISSライブラリを使用して高次元ベクトル(512次元)の顔特徴ベクトルから、類似していないデータを効率的に検索する手法を紹介します。
手法としては、以前紹介した「データセットから似ている顔を検索する」方法とは逆に、類似性の低いデータ(外れ値)を検出するアプローチです。
手順としては以下の5ステップになります。
- ベクトルの読み込みと前処理
- まず、顔画像から特徴ベクトルを抽出し、L2正規化を行います。L2正規化は、データのスケールを統一し、距離計算や類似性の計算を安定させるための手順です。また、正規化することで、内積ベースの類似度計算が可能になります。
- 各顔特徴ベクトルは、512次元のベクトルとして読み込まれますが、形状が
(N, 1, 512)のように余分な次元がある場合も考慮し、データの形状を(N, 512)に変換します。
- FAISSインデックスの作成とデータ追加
- FAISSの
IndexFlatIP(内積ベースのインデックス)を使用し、特徴ベクトルの検索インデックスを作成します。IndexFlatIPはデータセットが小規模な場合や、高速に内積ベースの検索を行いたい場合に適しており、直接データ追加後にすぐ使用できます。 - インデックスを作成し、全てのデータベクトルを追加することで、クエリ時に各ベクトル間の類似度(内積ベース)を計算できる状態になります。
- クエリベクトルとデータセット間の類似性計算
- 外れ値検出では、各データに対して他のデータとの類似度を計算し、特に類似度の低いデータを抽出することが目的です。
- コード内では、全データに対して類似度を計算し、類似度の高い上位k個のベクトル情報(近傍)を取得しています。その結果から、対象データ以外の近傍ベクトルとの類似度の平均を算出します。
- コサイン類似度の計算と外れ値判定
- FAISSで取得される類似度スコア(
Dの値)は内積に基づいているため、ベクトルが正規化された場合はコサイン類似度として解釈できます。この類似度を基に、閾値よりも類似度が低いデータを「外れ値」と判定します。 - コードでは、対象データ以外の近傍ベクトルとの類似度の平均が、設定した閾値(例えば0.3)を下回る場合に、該当データを「外れ値」として記録しています。
- 外れ値検出の具体的な判断基準と移動処理
- 閾値設定: 外れ値検出の閾値としてコサイン類似度が0.3未満のデータを外れ値としています。閾値はデータセットの特性に応じて調整可能です。
- 外れ値の保存処理: 外れ値として判定されたファイルは、指定のディレクトリ(
外れ値ファイル)に自動で移動されます。
npKnown.npzの作成
example/make_npKnown_file.pyを実行します。ドキュメントはこちらです。
作成されたnpKnown.npz

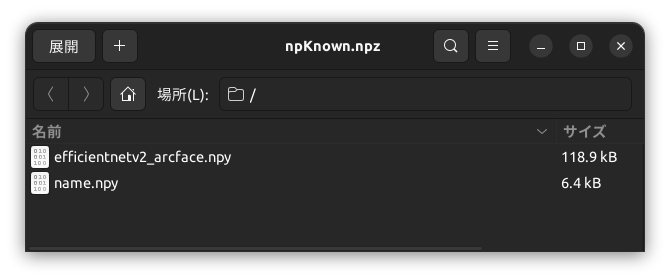
作成されたnpKnown.npzの中身は図のようになっています。efficientnetv2_arcface.npyに512次元ベクトルが、name.npyにファイル名が、それぞれバイナリの形で格納されています。
実装例とサンプルコード
ここでは、本文中で紹介した外れ値検出の手法のサンプルコードを提供します。コードはLOFとFaissを用いたものをそれぞれ作製しました。
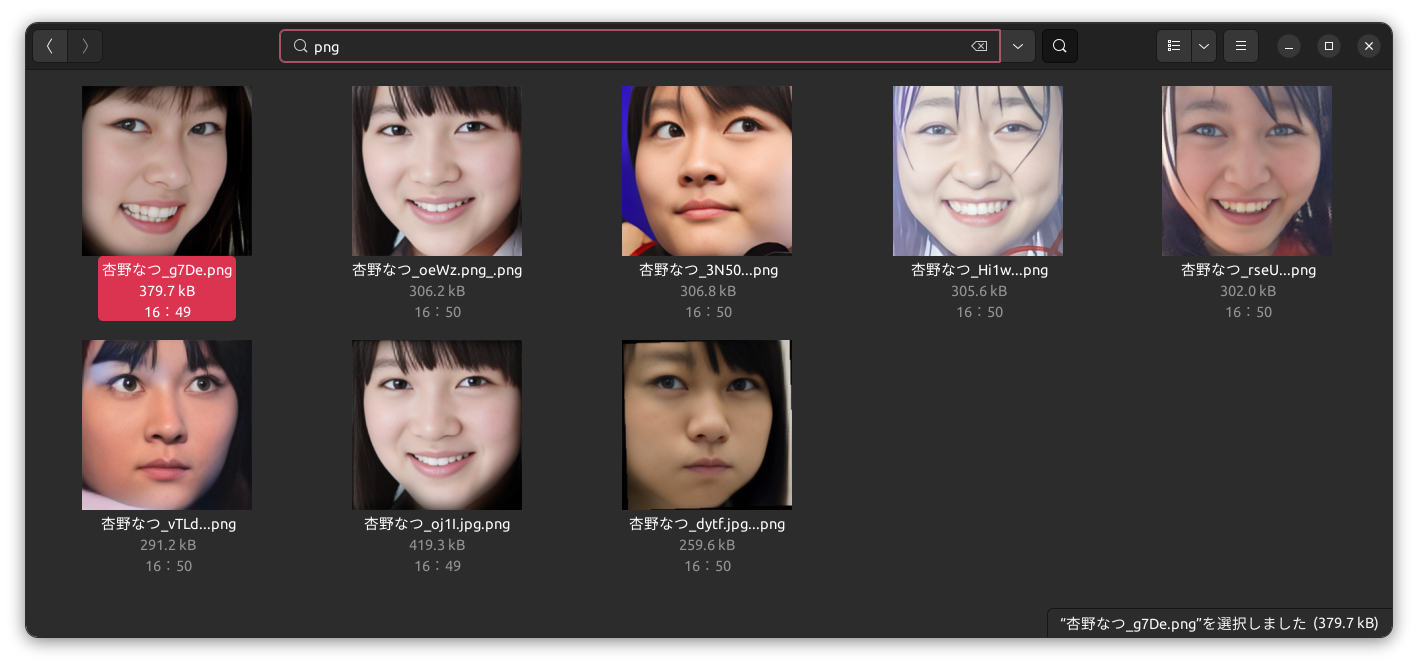
LOFによる外れ値ファイルの検出コード
LOFによる外れ値ファイルの検出の結果
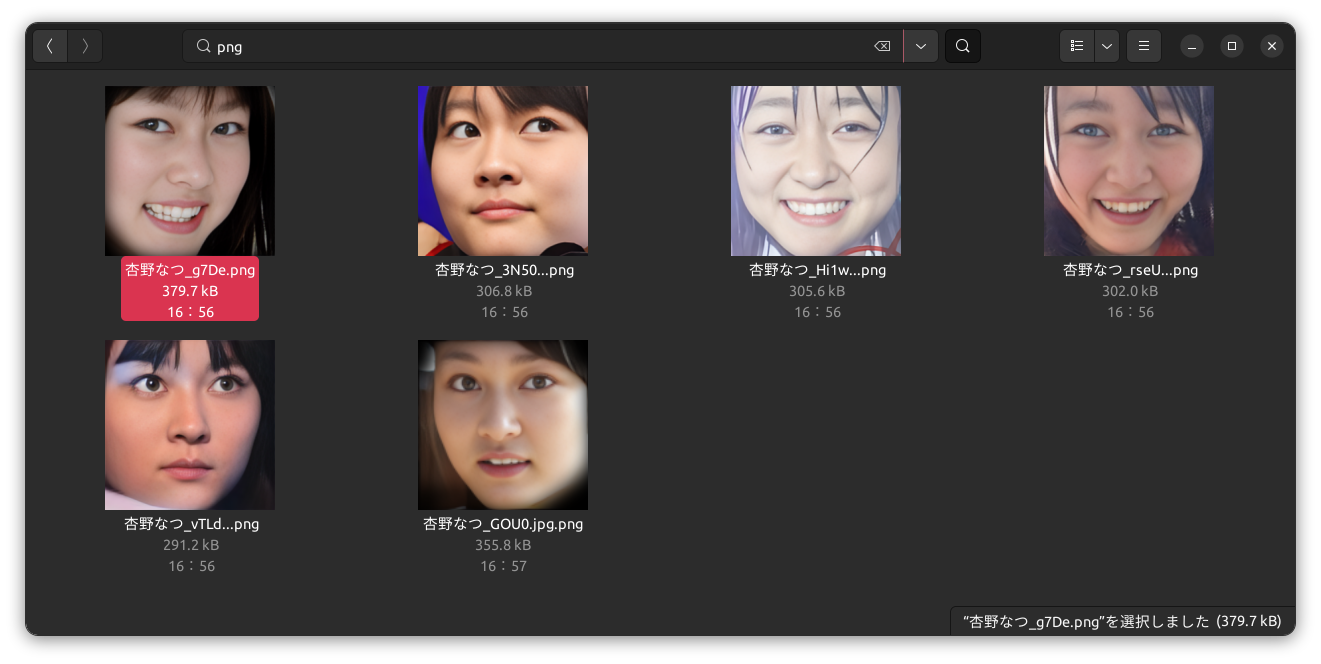
Faissによる外れ値ファイルの検出コード
Faissによる外れ値ファイルの検出の結果
さいごに
この記事ではクラスに紛れ込んだ外れ値をもつ画像ファイルを検出する概念とそれぞれのコードを紹介しました。LOFとFAISSの実装では、ほぼ同じファイルを検出することができました。


